DCA0445: Processamento Digital de Imagens

Matheus Petrovich <matheus.petrovich@gmail.com>

Lista de Exercício: Unidade II

Exercício 8: Filtragem no Domínio da Frequência

Esse projeto requer o desenvolvimento de um filtro Homomórfico, esse filtro tem o efeito de corrigir questões de iluminação na imagem e age no domínio da frequência. Ele realçar as altas frequências enquanto atenua as baixas frequências, o filtro tem um perfil como visto na função abaixo:

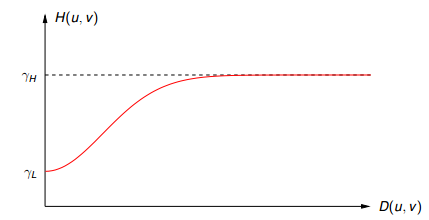
Figure 1. Perfil do Filtro Homomórfico

Podendo ser obtido por meio da seguinte expressão:

\$H(u,v) = (\gamma h - \gamma l)(1 - e^(-c (D^2(u,v))/D _0^2)) + \gamma l\$

Na expressão acima, D0, \$\gamma h\$, \$\gamma l\$ e c são variáveis que definem o comportamento do filtro, elas podem ser alteradas em tempo real por meio de sliders (figura "Saída do Programa"). Com o movimento dos sliders o filtro é recalculado pela função on_trackbar_config(int, void*) copiada abaixo:

filtroH.cpp

(...)
	void on_trackbar_config(int, void*){
		int M,N;
		float D2, dh, dl, d0;
		M = dft_M;
		N = dft_N;
		dh = dh_slider/10.0; (1)
		dl = dl_slider/10.0; (2)
		d0 = d0_slider/10.0; (3)

		tmp = Mat(dft_M, dft_N, CV_32F);
		for(int i=0; i<dft_M ;i++)
			for(int j=0; j<dft_N ;j++){
					D2 = ((float)i-M/2.0)*((float)i-M/2.0) + ((float)j-N/2.0)*((float)j-N/2.0);
					tmp.at<float>(i,j) = (dh-dl)*(1.0-exp(-1.0*(float)c_slider*(D2/(d0*d0))))+ dl;
				}
		Mat comps[]= {tmp, tmp};
		merge(comps, 2, filter); (4)
	}
(...)

¹ ² ³ Transforma o valor do slider do range 0-100 para 0-10, uma vez que o slider não permite valores decimais, e esses são desejados para o cálculo do filtro
⁴ Uma vez que a transformada de fourier da imagem é uma matriz com dois canais, o filtro precisa ser igual. Assim o H calculado em tmp é duplicado em filter que são ambas variáveis globais

O programa recebe como entrada o nome de uma imagem, a carrega em escala de cinza, tira o logarítmo da imagem para separar as componentes de reflectância e iluminância de uma multiplicação pra uma soma, calcula a Transformada de Fourier, troca os quadrantes de modo que o sinal fique com a origem no centro da figura. Após aplicar o filtro no domínio da frequência (multiplicação das duas matrizes editadas por meio de padding para que tenham tamanhos iguais) os quadrantes são destrocados, a imagem é normalizada com o propósito de diminuir a amplitude dos dados trazendo-os para o intervalo de 0-1. A imagem então passa a Transformada de Fourier inversa e então é feita a exponencial da imagem de saída, seguida de uma segunda normalização. Exemplo de input pode ser visto na imagem abaixo:

Figure 2. Exemplo de imagem com problemas de iluminação

Sua transformada de Fourier tem a seguinte forma:

Figure 3. Transformada de Fourier

O filtro que deu o melhor resultado foi o abaixo:

Figure 4. Filtro Homomórfico

Como pode ser visto, a região central, que multiplica as baixas frequências do espectro da imagem, é mais escura, com valores mais próximos do zero, fazendo a atenuação das baixas frequências. As demais regiões brancas mantém a relevância das altas frequências. A seguir pode ser visto o espectro da imagem filtrado:

Figure 5. Espectro Fitrado

A saída do programa, juntamente com os parâmetros que geraram o filtro da Figura "Filtro Homomórfico" pode ser vista abaixo:

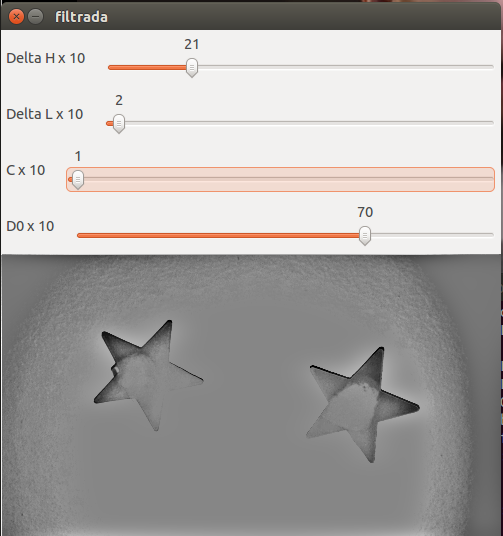
Figure 6. Saída do Programa

Um comparativo das imagens de entrada e saída:

Figure 7. Comparativo da Entrada com a Saída

Como pode ser visto acima, nenhuma informação nova é criada, mas a iluminação da imagem e seu brilho ficam mais uniformes mediante a filtragem.

O código na íntegra pode ser visto aqui

Exercício 11: Filtro de Canny e Pointilhismo

O propósito deste exercício é utilizar o algoritmo de Canny para detecção de bordas para processar uma imagem simulando que foi feita por meio da técnica de pintura pontilhista. O algoritmo de Canny tem os seguintes passos:

Filtragem com filtro Gaussiano para redução de ruídos
Cálculo do gradiente dos pixels da imagem
1. Classificação dos pixels nas seguintes categorias: Horizontal, Vertical, \$+45^\circ\$ e \$-45^\circ\$
2. Comparação da magnitude do gradiente dos pixels com os de seus vizinhos na direção da etapa acima, se sua magnitude for a maior, ele é mantido na imagem de saída como pixel de borda, se não, é descartado
Limiarização
1. O filtro tem dois parâmetros, T_H e T_L, sendo T_H entre 2 e 3 vezes T_L
2. Se a magnitude do gradiente do pixel for maior que T_H, esse pixel é de borda forte e pertence à borda
3. Se ela for menor que T_L, o pixel é descartado
4. Se a magnitude estiver entre T_H e T_L, então ele é de borda fraco. Seus 8 vizinhos serão investigados, se algum dos vizinhos for de borda forte, então ele também passa a ser, caso contrário será descartado

O projeto a seguir descrito foi baseado nas referências do professor Agostinho Brito Jr. encontradas aqui

A imagem usada como entrada para os testes aqui descritos foi a seguinte:

O programa desenvolvido segue os seguintes passos:

Carrega imagem de entrada
Itera sobre a imagem de entrada escolhendo pontos baseado em um passo estabelecido, e colocando na imagem de saída circulos com a cor do ponto centrado a uma pequena distância (gerada randomicamente) do centro do ponto, para dar um efeito mais próximo da falha humana e reduzir a simetria típica do computador. As principais diferenças do código original do pontilhismo foram a adaptação para imagem colorida e o multiplicador (também randômico) para alterar levemente a cor, quebrando um pouco a continuidade da coloração, dando um efeito mais artesanal. Para isso foi necessário alterar a iniciação da matriz points e fazer algumas mudanças nos laços que podem ser vistas abaixo:

cpts.cpp

(...)
	points = Mat(height, width, CV_8UC3, Scalar(255,255,255)); //agora points é colorida
	random_shuffle(xrange.begin(), xrange.end());
	for(auto i : xrange){
		random_shuffle(yrange.begin(),yrange.end());
		for(auto j : yrange){
		  x = i+rand()%(2*jitter)-jitter+1;
		  y = j+rand()%(2*jitter)-jitter+1;
			passo = (rand()%2)/10.0 +1.0; //cria uma constante multiplicativa pra variar a cor
		  val[0] = min((int)(image.at<Vec3b>(x,y)[0]*passo),255); // varia a cor, e não deixa que o valor passe de 255
		  val[1] = min((int)(image.at<Vec3b>(x,y)[1]*passo),255);
		  val[2] = min((int)(image.at<Vec3b>(x,y)[2]*passo),255);
		  circle(points,
		         cv::Point(y,x),
		         raio,
		         cv::Scalar(val[0],val[1],val[2]),
		         -1);
		}
	}
(...)

A imagem abaixo foi obtida:

Em seguida, o algoritmo de Canny será rodado iterativamente na imagem, com constantes crescentes e em cada iteração a imagem de saída será varrida, onde houver bordas, novos círculos serão inseridos na imagem de saída. Dessa vez foi inserida uma variação randômica no raio dos circulos, novamente para quebrar um pouco da simetria da máquina.

cpts.cpp

(...)
	for(int i=1; i<160 ;i+=20){
			Canny(image, border, i, 3*i);

			for(int l=3; l<height-3 ;l++)
				for(int c=3; c<width-3 ;c++){
					if(border.at<uchar>(l,c) == 255){
						raio = 1+rand()%3;
						passo = (rand()%2)/10.0 +1.0;
						x = l+rand()%(2*jitter)-jitter+1;
			 			y = c+rand()%(2*jitter)-jitter+1;
						val[0] = min((int)(image.at<Vec3b>(x,y)[0]*passo),255);
						val[1] = min((int)(image.at<Vec3b>(x,y)[1]*passo),255);
						val[2] = min((int)(image.at<Vec3b>(x,y)[2]*passo),255);
						circle(points,
								   cv::Point(y,x),
								   raio,
								   cv::Scalar(val[0],val[1],val[2]),
								   -1);
					}
				}
	}
(...)

Para valores baixos dos limiares, muitos pontos são aceitos para a borda:

A saída acima aplica sobre a imagem esses pontos:

Um limiar intermediário já tem a seguinte saída:

Um limiar mais alto tem a seguinte saída:

O resultado final foi a imagem abaixo:

O código na íntegra pode ser visto aqui